阶乘计算升级版
本题目出自于拼题A,基础编程题6-10. 阶乘计算升级版 (20 分)
该题要求实现一个打印非负整数阶乘的函数。
函数接口定义:
1 | |
其中N是用户传入的参数,其值不超过1000。如果N是非负整数,则该函数必须在一行中打印出N!的值,否则打印“Invalid input”。
裁判测试程序样例:
1 | |
输入样例:
1 | |
输出样例:
1 | |
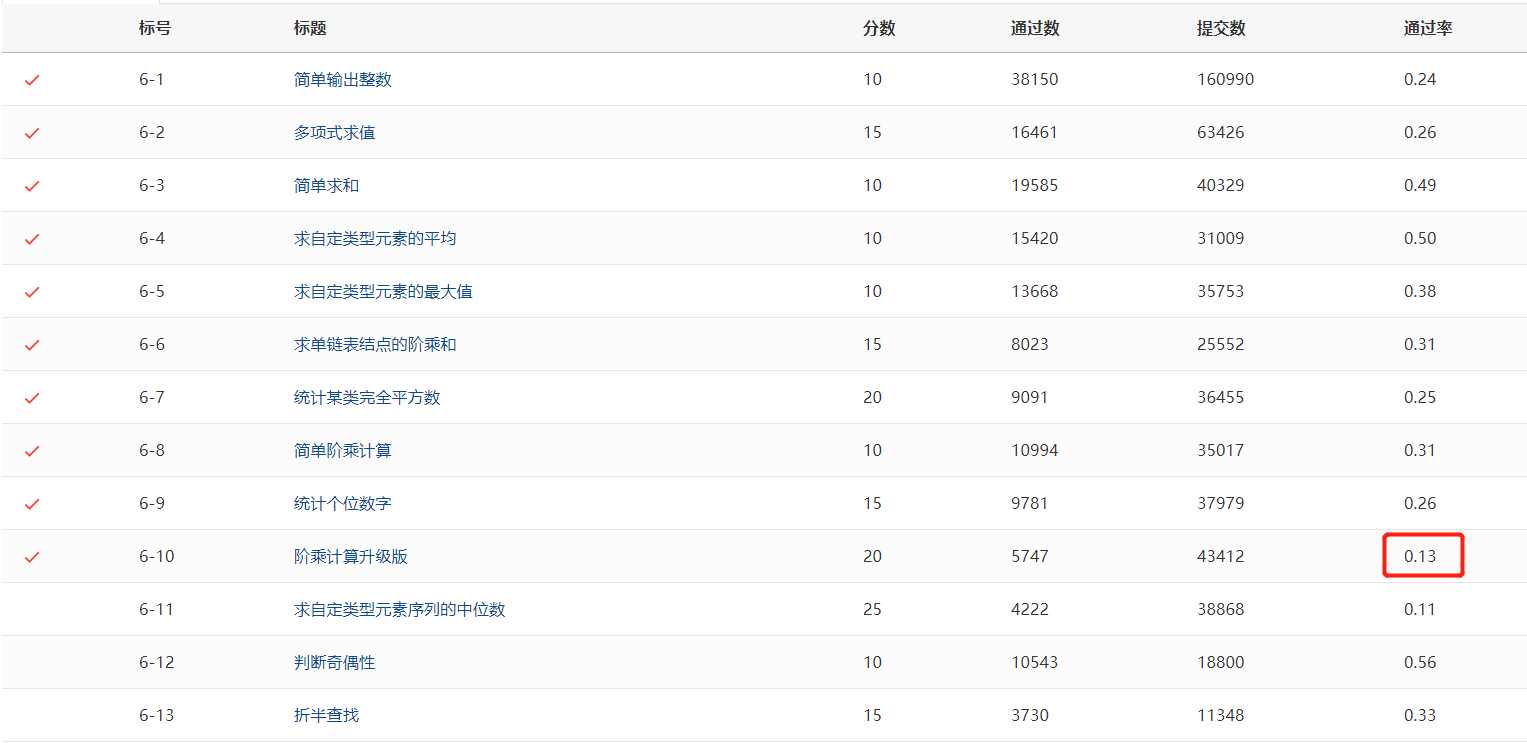
这道题目的通过率仅为0.13,属于较难的题目。其难点主要在于:
- 需要要计算大数乘法。由于int类型的范围包含4个字节,排除最高位符号位,其十进制最大可表示的数字是2,147,483,647(即2的31次方-1),超过该数就会出现栈溢出问题。用计算器计算一下可以发现,12!= 479,001,600 < 2,147,483,647,它用最简单的递归或者循环来做,没有问题。但是13!= 6,227,020,800 > 2,147,483,647,出现栈溢出。
- 必须要使用数组来逐位计算数字乘法,同时考虑进位问题。
解题思路:
① 定义一个数组result[ ]用来装阶乘结果。考虑N最大可以取1000,而1000^1000=10^3000 >> 1000!,因此将数组的长度设为3000位绰绰有余。
数组result[ ]的角标由小到大可以依次表示结果的低位到高位,最终输出结果,由大角标到小角标输出即可。
② 分别定义两个指针i和h,i表示当前运存所处的位置,j表示当前运算结果最高位的位置。
③ 每次做乘法,都是用当前阶乘元素n与当前位置i的值做乘法,同时,加上前一位保存的进位数carry。运算结果保存在outcome中。每次结束,指针i向后移动一位,继续计算乘积和加法,直到i与h重合,该轮乘法计算结束。
③ 如果运算至最高位(i与h重合)时,carry>0,则需要向更高位进位,因此h向后移动。具体移动多少位,由carry的值决定(carry的值可能大于10)。
1 | |
运行结果如下: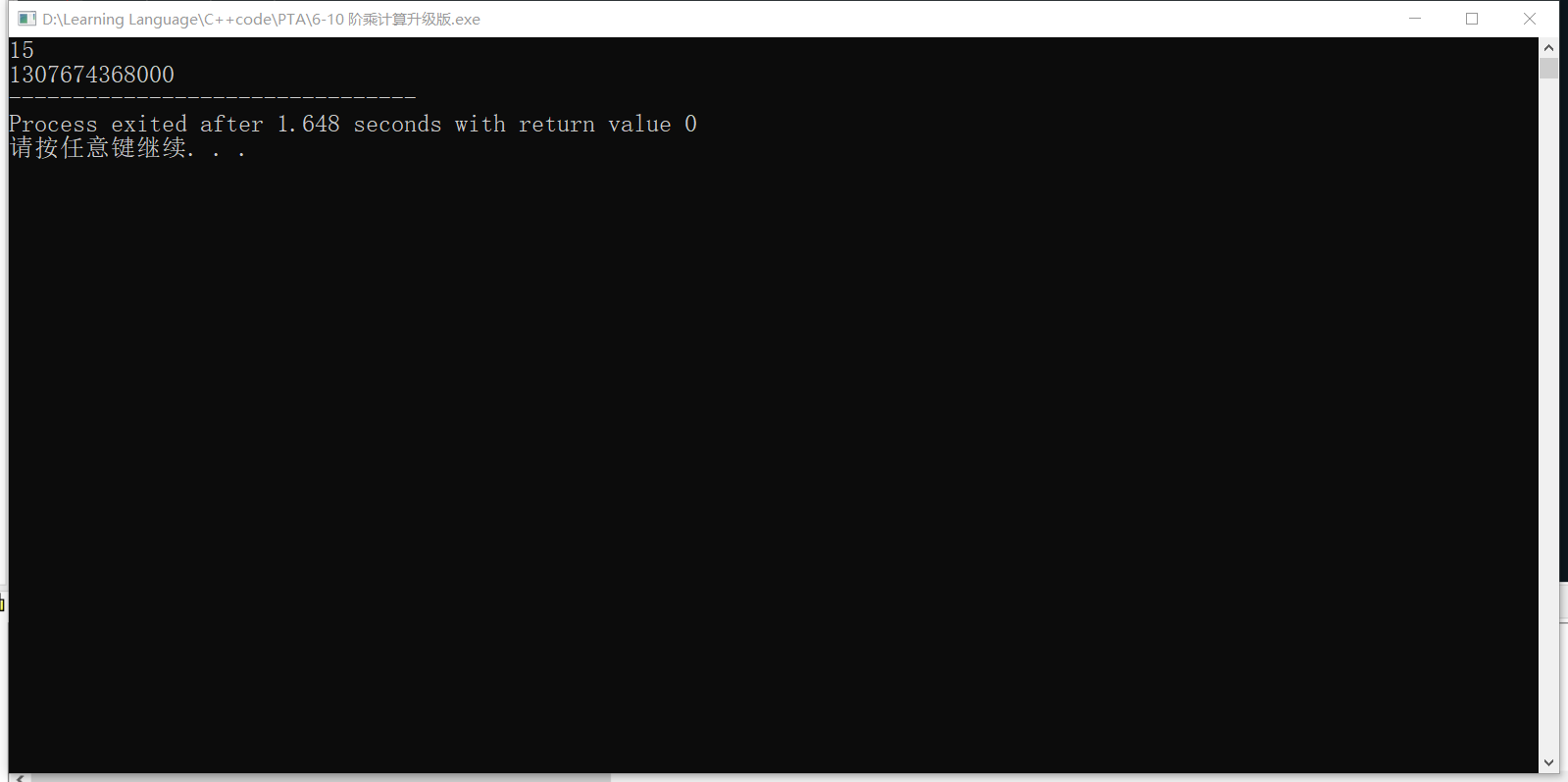
计算1000的阶乘没有问题: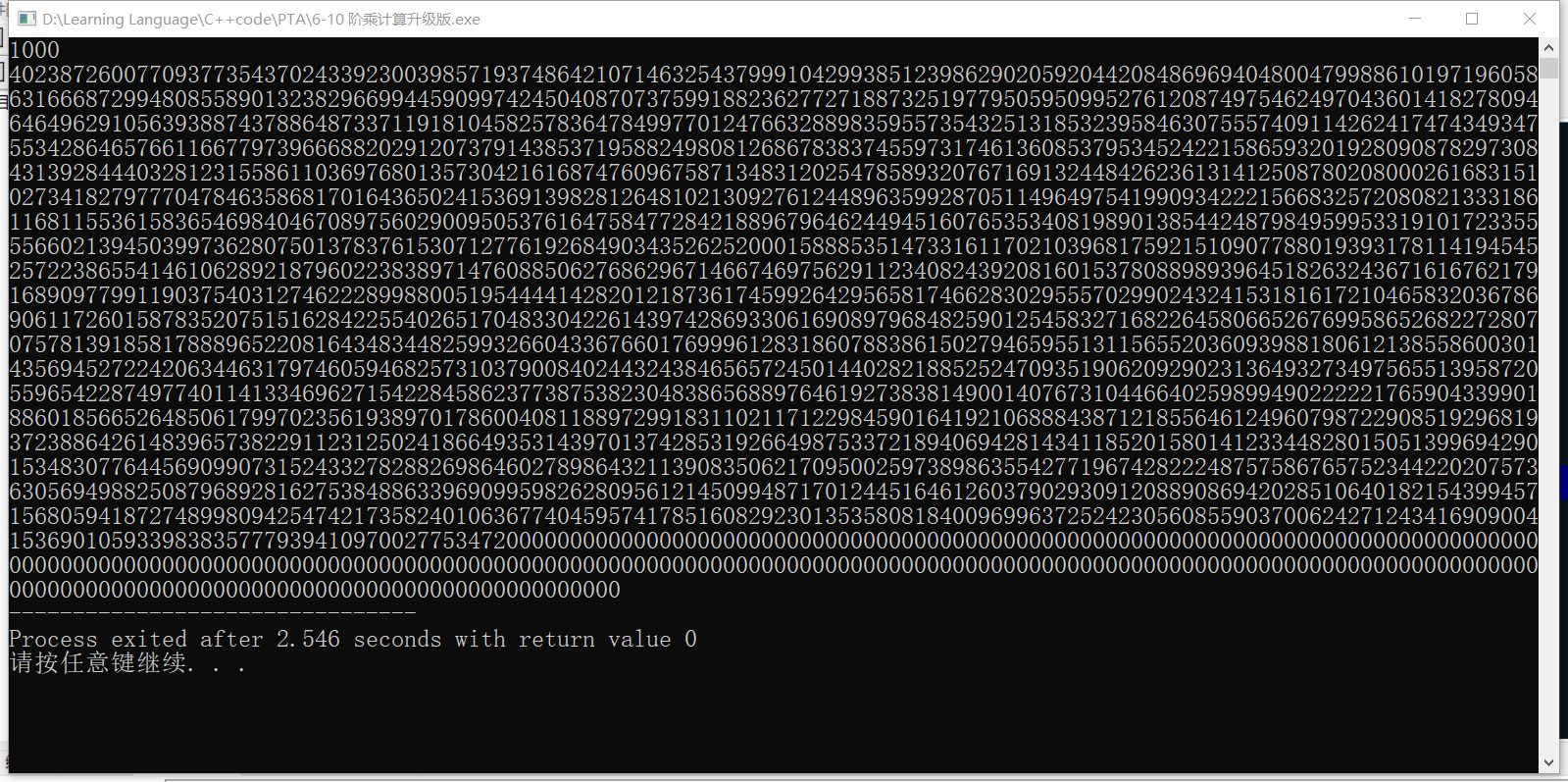
提交结果完全正确: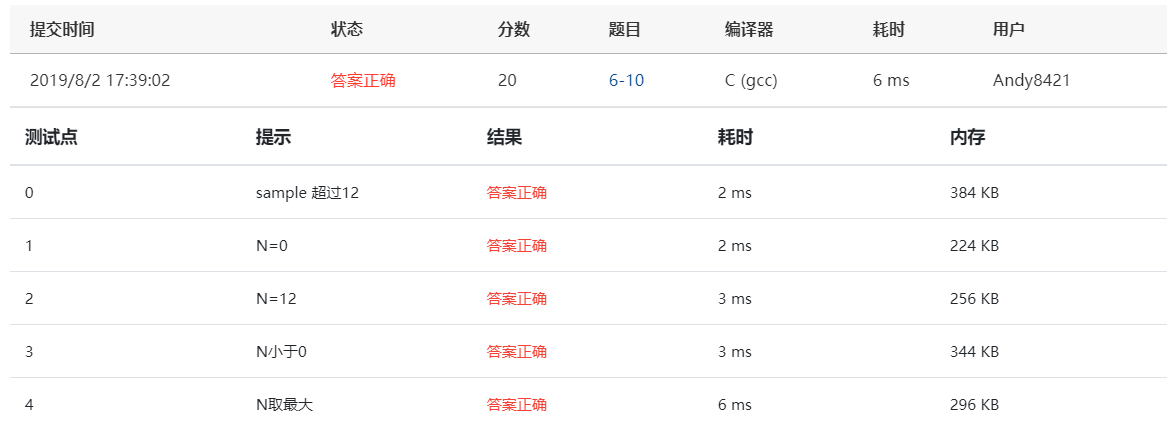
版权声明:本文作者为「Andy8421」.本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!